New in CGAL: Optimal Bounding Box

Konstantinos Katrioplas, Mael Rouxel-Labbé

GeometryFactory

Encompassing a model within a volume is a common approach to accelerate a number of applications such as collision detection or visibility testing: the proxy volume provides a rapid way to test a configuration or filter results, with the real model only being used when required. Typical coarser volumes that can be used to approximate a more complex model are simplified meshes (for example using the package Surface Mesh Simplification), convex hulls, or simple rectangular boxes.

Bounding Volumes

Within bounding boxes, the axis-aligned bounding box (AABB) has obvious advantages: it is extremely simple to compute and one may build a hierarchical structure of successively tighter volumes to further speed up intersection and distance computations. One such structure is the AABB tree. The disadvantage is also clear: the box is usually poorly fitting most models. A good compromise between the good approximation offered by convex hulls or simplified meshes and the speed offered by axis-aligned bounding boxes are Optimal Bounding Boxes. Contrary to the AABB, the optimal bounding box of a model is not necessarily axis-aligned, but provides a tight approximation.

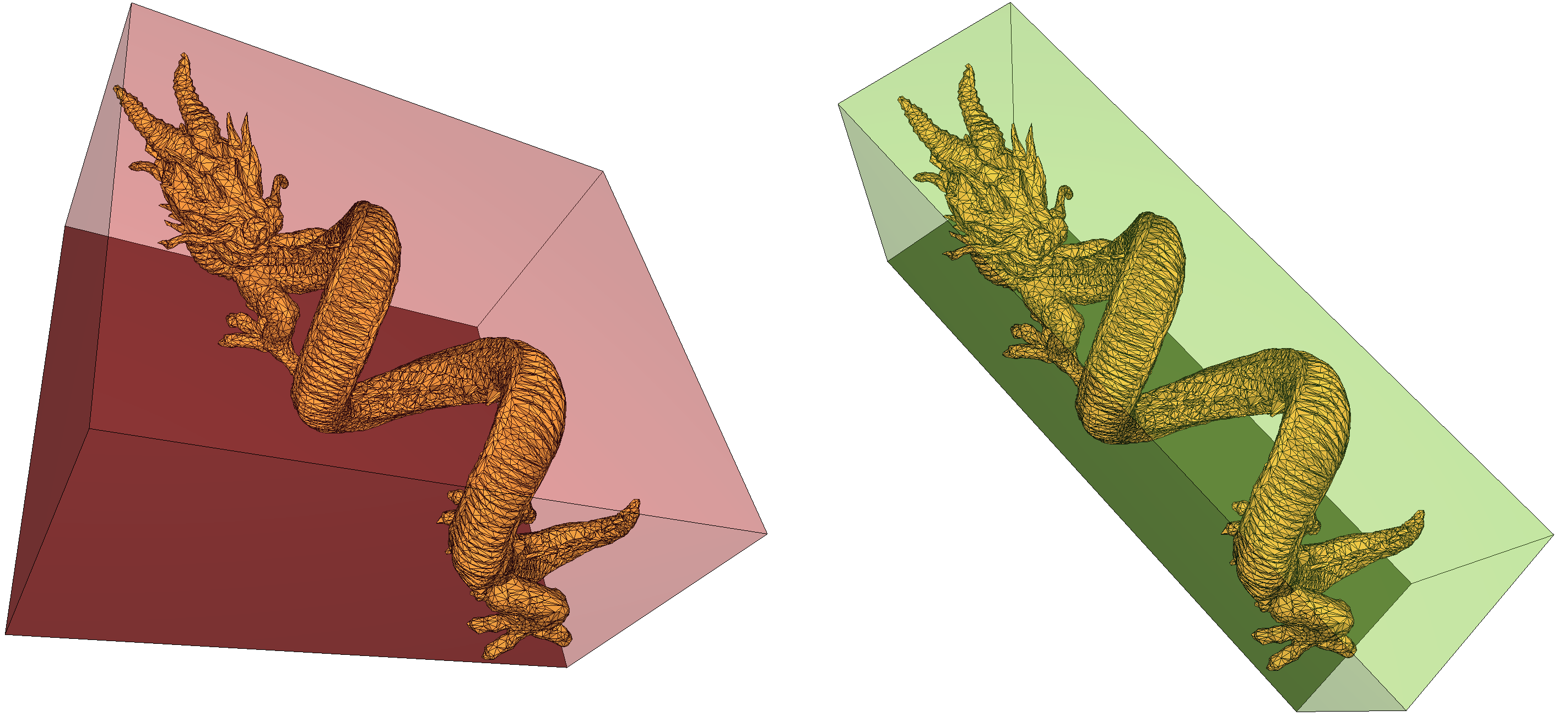
Although simple to compute, an AABB (left) is rarely as a good fit for a model as the optimal bounding box (right)

Optimal Bounding Box

In 2D, the optimal bounding rectangle of an input can be computed in linear time using the technique of rotating calipers (see also the CGAL package Bounding Volumes). An algorithm to compute the optimal oriented bounding box in 3D was proposed by O’Rourke in 1985 (Finding Minimal Enclosing Boxes), but its cubic complexity in the number of points makes it unusable in practice.

The implementation proposed in this new CGAL package is based on the paper of Chang et al., Fast oriented bounding box optimization on the rotation group SO(3, R), where an algorithm to compute a close approximation of the optimal bounding box is introduced. The algorithm formulates the computation of the optimal bounding box as an unconstrained optimization problem on the 3D matrix rotation group. The function to optimize is defined as the volume of the box. Because this function is non-differentiable, in particular near local optima, traditional optimization methods might encounter convergence issues. Consequently, Chang et al.'s algorithm employs a combination of a derivative-free optimization method, the Nelder-Mead simplex method, and a metaheuristics method based on biological evolution principles to maintain and evolve a population of tentative rotation matrices. The purpose of this evolution is to oppose a global approach to the local Nelder-Mead optimization, enabling the algorithm to explore the search space as much as possible, and to find not only a local minimum, but a global optimum.

Implementation in CGAL

The implementation of CGAL supports point sets and meshes as input, with multiple possible output types. Convex hull preprocessing is used to greatly improve speed, and is performed using the package 3D Convex Hull.

Optimal bounding boxes of a set of chess pieces.

The package Optimal bounding box is already integrated in CGAL's master branch on the CGAL GitHub repository, and will be officially released in the upcoming version of CGAL, CGAL 5.1, scheduled for July 2020.